How To: Find a P-Value with Excel

So you need to find the p-value for your hypothesis test. To do so, employ the spreadsheet program Microsoft Excel. Using a simple formula, you can easily determine the p-value for your tests and thereby conclude strong or weak support of the null hypothesis.

Probability values, or p-values, were popularized in the 1920s in statistics, though they've been around since the late-1700s. This value, which determines the "significance of results" in hypothesis testing, is used in various fields, from economics to criminology. In short order, it tells us the how strong a claim or null hypothesis is. Will the null hypothesis be proven out? Or will it be rejected in favor of the alternative hypothesis? The answer lies with the p-value(s).

P-Value Formula & Arguments

As said, when testing a hypothesis in statistics, the p-value can help determine support for or against a claim by quantifying the evidence.

The Excel formula we'll be using to calculate the p-value is:

• =tdist(x,deg_freedom,tails)

Where the arguments are:

• x = t
• deg_freedom = n-1 (degrees of freedom)
• tails = 1 for a one-tail test or 2 for a two-tail test

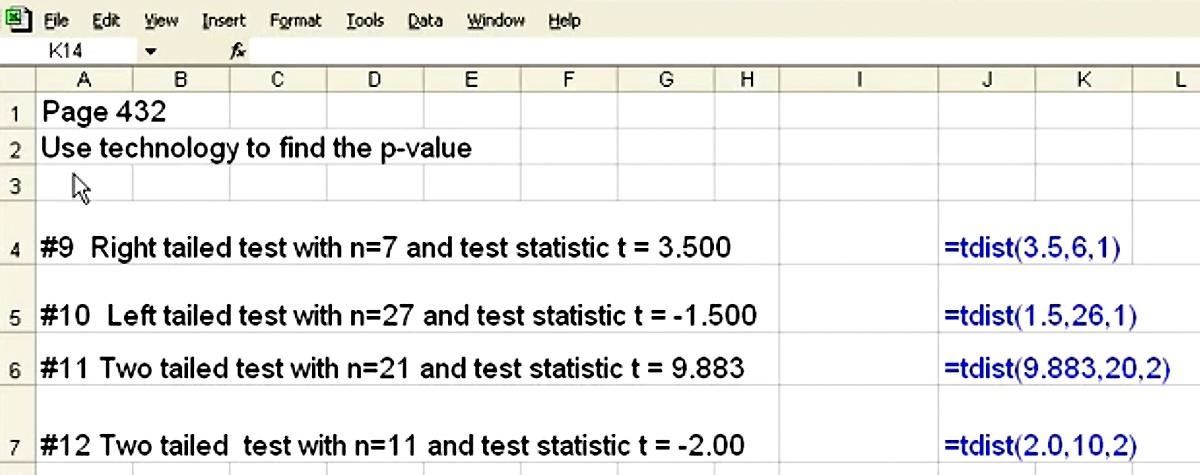
Significance Level & Testing

A common significance level used is 0.05, which says that if the resultant p-value is equal to or less than 0.05, then there's strong evidence against the null hypothesis (and enter the alternative hypothesis). If the p-value is greater, then the null hypothesis has merit.

And so to solve the p-value in an Excel spreadsheet, simply select a cell and type in =t-dist( to bring up the formula and then type in the arguments, separating each by a comma:

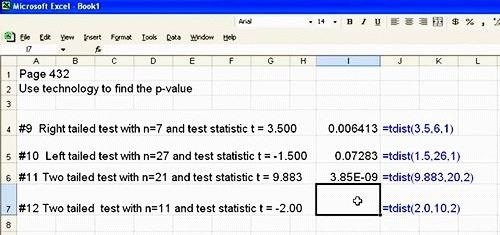
If we use 0.05 as the significance level, then from this set, what do we find? Considering the calculated p-values in column I in our examples above, we can conclude that all tests but the first (p-value = 0.006413) have strong evidence in favor of the null hypothesis.

Pretty cool. Ready to carry out some hypothesis testing of your own? As you fire up the Excel, check out the original tutorial below by YouTube user meaniefiene. While it's seen using an older version of Excel, the function works the exact same way on newer versions, no matter if you're using Excel on a Windows or Mac computer.